Solitary waves in 1-D granular materials
F. Santibañez, F. Tapia, S. Job, F. Melo

Figure 6. Experimental setup, upper panel shows a general view of the setup. Lower left panels, show some details on the sensor placement and one of the releasing devise of the striker bead. Lower right panel gives a perspective view of the experimental setup'
We explore experimentally and numerically the propagation of shock waves in 1 dimensional chain of elastic beads. Various types of configurations have been studied, beginning with the chain of identical beads which shows how the shock wave is propagated in the form of a solitary wave, with well defined speed and duration, as can be seen in inserts (b-c) in figure 1. We have used this solitary wave to study the elastic module (Young modulus) of some rigid samples [1].
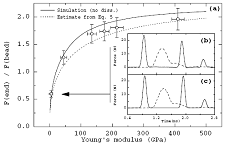
Figure 1. (a) Ratio of force amplitude at the end of the chain and of the incident impulse vs Young’s modulus of the sample placed on the rigid sensor.
We have also studied the propagation of this solitary wave when there is a step change in the bead size along the chain, named stepped chain, where the first part has a bead diameter D, and the second has a bead diameter d, with D>d. Experimental and numerical results shows how we can relate the number of solitary waves in the solitary wave train formed after the main solitary waves passes from the first part to the second with the number of beads that are compressed in the transmission process[2].
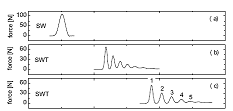
Figure 2. (a) Force measured at the end of the monodisperse chain. (b-c) Force meassured at the middle and end of the stepped chain, this figure shows the formation of a Solitary wave train, from a single incident solitary wave
Tapered chains have also been studied; we found that when the solitary wave propagates along a chain where the bead diameter is exponentially decreased, the amplitude of the shock wave decreases along the chain, becoming this kind of system of particular interest as a shock absorption device [3].
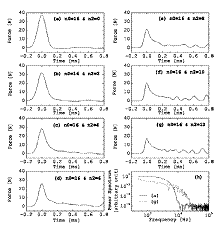
Figure 3. (a) Force measured at the end of the monodisperse chain. (b-g) Force felt at the right contact of bead Nos. 18, 20, 22, 24, 26 in the decreasing part of the tapered chain. (h) Power spectrum indicating a comparison between incoming and outcoming pulses in the tapered chain.
The presence of a small intruder inside the chain has also been studied. This problem has shown us that with simple physical arguments we can describe the nature of the phenomena. Localized oscillations of the intruder when the solitary wave passes have been understood using the simple mass-spring model, giving as a result a power law wish relates the localized oscillation's frequency with the size of the intruder and the force felt by it [4]. This simple relation has been found to correspond with numerical and experimental results.
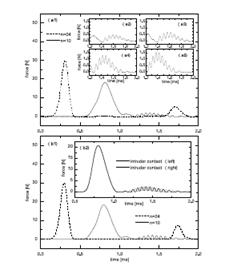
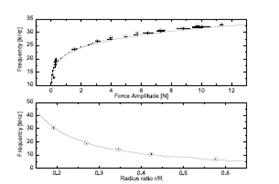
Figure 5.The left panel shows the actual force measured at the intruder’s contact. The right panel indicates the comparison between experimental data and theoretical power law.
A recently started work is the interaction of two solitary waves that propagates along the chain of identical beads in opposite directions, the experimental set up for this particular experiment is still in development due to the great number of parameters that affect the propagation of both solitary waves and the sensibility needed to capture the physical phenomena of interest.
On going research
Stepped chain under external load, the following images present the experimetal setup.
Figure 6.The upper panel shows a lateral view of the experimental setup, the middle panels shows details on the wall sensor and the bead sensor. the lower panels shows detail of the bead's ring, and the two right panels shows details of the cap, designed to control the load applied on the chain. (Click on each image for a large version)
[1] Job, S., Melo, F., Sokolow, A., and Sen,S., "How Hertzian solitary waves interact with boundaries in a 1D granular medium". Phys. Rev. Lett. 94, 178002, (2005)
[2] Job, S., Melo, F., Sokolow, A., Sen, S., "Solitary wave trains in granular chains: Experiments, theory and simulations". Submitted to Granular Matter (2007)
[3] Melo, F., Job, S. , Santibañez, F., Tapia, F., "Experimental evidence of shock mitigation in a Hertzian tapered chain", Phys. Rev. E. 73, 041305, (2006)
[4] Job, S., Santibañez, F., Tapia, F., and Melo, F., "Experimental Evidence of Localized oscillations in Hertzian chains". Submitted to Phys. Rev. Lett. (December 2006).






